Time Series Forecasting with XGBoost

Utilizando Machine Learning Forecast

XGBoost
MLForecast
Python
sklearn
Author

Juan Isaula

Published

August 7, 2023

MLForecast

MLForecast es un marco de datos para realizar pronósticos de series de tiempo utilizando modelos de aprendizaje automático, con la opción de escalar a cantidades masivas de datos utilizando clústeres remotos.

¿Por qué utilizar MLForecast?

Las alternativas actuales de Python para los modelos de aprendizaje automático son lentas, imprecisas y no escalan bien. Así que se crearón una biblioteca que se puede usar para hacer pronósticos en entornos de producción. MLForecast incluye ingeniería de características eficientes para entrenar cualquier modelo de aprendizaje automático (con fit y predict métodos como sklearn) para adaptarse a millones de series temporales.

Características

  • Las implementaciones más rapidas de ingeniería de funciones para la previsión de series temporales en Python.

  • Compatibilidad lista para usar con Spark, Dask y Ray

  • Pronósticos probabilísticos con predicción conforme.|

  • Soporte para variables exógenas y covariables estáticas.

  • Sintaxis familiar sklearn: .fit y .predict

Validación Cruzada

La validación cruzada de series temporales es un método para evaluar cómo se habría comportado un modelo en el pasado. Funciona definiendo una ventana deslizante a través de los datos históricos y prediciendo el período que le sigue.

MLForecast tiene una implementación de validación cruzada de series de tiempo que es rápida y fácil de usar. Esta implementación hace que la validación cruzada sea una operación eficiente, lo que hace que consuma menos tiempo.

¿Cómo realizar validación cruzada de series de tiempo?

Una vez que se ha instanciado el objeto MLForecast, podemos usar el método cross_validation, que toma los siguientes argumentos:

  • data: marco de datos de entrenamiento con formato MLForecast.

  • window_size(int): representa los h pasos hacia el futuro que se pronosticarán

  • n_windows (int): cantidad de ventanas utilizadas para la validación cruzada, es decir, la cantidad de procesos de pronóstico en el pasado que desea evaluar.

  • id_col: identifica cada serie temporal

  • time_col: identifica la columna de la serie temporal

  • target_col: identifica la columna a modelar

El objeto crossvaldation_df es un nuevo marco de datos que incluye las siguientes columnas:

  • unique_id: identifica cada serie temporal

  • ds: marca de fecha o índice temporal

  • cutoff: la última marca de fecha o índice temporal del n_windows

  • model: columnas con el nombre del modelo y el valor ajustado.

Evaluar Resultados

Una vez hecho todo lo anterior, podremos calcular la precisión del pronóstico utilizando una métrica de precisión adecuada. En mi caso particular uso el error cuadrático medio (RMSE). Para hacer esto, primero debemos instalar datasetsforecast, una biblioteca de Python desarrollada por Nixtla que incluye una función para calcular el RMSE.

La función para calcular el RMSE toma dos argumentos:

  1. Los valores reales
  2. Las predicciones

Esta medida debería reflejar mejor las capacidades predictivas de nuestro modelo, ya que utilizo diferentes periodos de tiempo para probar su precisión.

Modelo XGBoost

El modelo XGBoost es un algoritmo de aprendizaje automático supervisado basado en árboles de decisión. Se utiliza para problemas de regresión y clasificación, se ha convertido en uno de los modelos más importantes y efectivos en las competencias de aprendizaje automático.

Toerema del Modelo XGBoost

Dados los datos de entrenamiento \(D = (x_1, y_1), (x_2, y_2), . . . , (x_n, y_n)\) donde cada \(x_i\) es un vector de características de entrada y cada \(y_i\) es la etiqueta de salida correspondiente, el objetivo es encontrar una función \(f(x)\) que mapee los vectores de características a las etiquetas de salida y minimice el error de predicción en el conjunto de entrenamiento.

La construcción del modelo implica la creación de un conjunto de árboles de decisión, donde cada árbol se construye de manera secuencial para minimizar la función de costo global, que es la suma de las funciones de costo individuales de cada árbol.

El algoritmo XGBoost también utiliza técnicas de regularización para evitar el sobreajuste, lo que ayuda a mejorar el rendimiento en conjuntos de datos no visto. Estás técnicas incluyen la poda de árboles, la penalización \(L_1\) y \(L_2\), y el muestreo aleatorio de observaciones y variables.

Una característica del modelo XGBoost es que puede trabajar con tados a lo bruto (es decir, bases que contengan datos faltantes), es tan robusto que puede trabajar con este tipo de datos.

Modelo XGBoost Matemáticamente

El modelo XGBoost se construye a través de una combinación de árboles de decisión y técnicas de optimización de gradiente. En términos matemáticos el modelo XGBoost se puede escribir como:

\[ f(x) = \sum T(x;\theta_j) \]

donde \(f(x)\) es la función de predicción para el conjunto de características de entrada \(x\), \(T(x;\theta_j)\) es un árbol de decisión con parámetros \(\theta_j\), y la suma se realiza sobre un conjunto de árboles de decisión.

Cada árbol de decisión se construye de manera secuencial para minimizar la función de costo global, que es la suma de las funciones de costo individuales de cada árbol, es decir:

\[L = \sum l(y_i,f_i(x_i)) + \sum \Omega(\theta_j)\]

donde \(l(y_i, f_i(x_i))\) es la función de costo para el i-ésimo ejemplo de entrenamiento, \(f_i(x_i)\) es la predicción del modelo para el i-ésimo ejemplo de entrenamiento,y \(\Omega(\theta_j)\) es la penalización para el j-ésimo árbol de decisión, diseñada para evitar el sobreajuste.

La función de costo se puede escribir de varias maneras, dependiendo del problema específico. Por ejemplo, en un problema de regresión, la función de costo podría ser el error cuadrático medio (MSE), mientras que en un problema de clasificación, la función de costo podría ser la antropía cruzada.

Para construir el modelo XGBoost, se utilizan técnicas de optimización de gradiente para minimizar la función de costo global. Estas técnicas implican calcular las derivadas de la función de costo con respecto a los parámetros del modelo, y ajustar los parámetros en consecuencia.

Además, XGBoost utiliza técnicas de regularización para evitar el sobreajuste, como la poda de árboles, la penalización \(L_1\) y \(L_2\), y el muestreo aleatorio de observaciones y variables.

En resumen, el modelo XGBoost se construye a través de una combinación de árboles de decisión y técnicas de optimización de gradiente, con el objetivo de minimizar la función de costo global mientras se aplica la regularización para evitar el sobreajuste.

XGBoost para series de tiempo

XGBoost también puede ser aplicado a problemas de series de tiempo. Sin embargo, es importante tener en cuenta que la aplicación del modelo a datos de series de tiempo requiere un enfoque ligeramente diferente en comparación con los problemas de clasificación y regresión estándar.

Para aplicar XGBoost a datos de series de tiempo, es necesario crear características adecuadas para el modelo, lo que puede incluir características basadas en ventanas moviles, diferencias y tasas de cambio. También es importante considerar la estacionalidad y las tendencias en los datos de series de tiempo y aplicar técnicas de preprocesamiento de datos y validación cruzada adecuadas para este tipo de problemas.

Además, se deben tener en cuenta algunas consideraciones especiales en la configuración de características relevantes para la serie de tiempo y la selección de la función de costo y métricas de evaluación adecuadas.

Caso de estudio

Librerías

# 1. Manipulación y Tratamiento de Datos
import numpy as np
import pandas as pd

# Convertir a un formato de datetime 
from datetime import datetime 

# Ocultar Warnings
import warnings 
warnings.filterwarnings("ignore")

# 2. Modelación XGBoost
import xgboost as xgb
from mlforecast import MLForecast
from mlforecast.target_transforms import Differences
from sklearn.ensemble import RandomForestRegressor
from numba import njit
from window_ops.expanding import expanding_mean
from window_ops.rolling import rolling_mean

# 3. Métricas para evaluación del modelo 
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import r2_score
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score, KFold

# 4. Gráficos o Plots
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
import plotly.express as px
import plotly.graph_objects as go
import seaborn as sns
plt.style.use("fivethirtyeight")
plt.rcParams["lines.linewidth"] = 1.5
dark_style = {
    "figure.facecolor": "#212946", "axes.facecolor": "212946",
    "savefig.facecolor":"212946", "axes.grid":True,"axes.grid.which": "both",
    "axes.spines.top": False, "axes.spines.bottom": False,"grid.color": "#2A3459",
    "grid.linewidth": "1", "text.color":"0.9", "axes.labelcolor": "0.9",
    "xtick.color": "0.9", "ytick.color": "0.9", "font.size": 12}
plt.rcParams.update(dark_style)

# Tamaño del gráfico 
from pylab import rcParams
rcParams["figure.figsize"] = (8,5)

Data

Como ya lo he mencionado, la entrada a MLForecast siempre es un marco de datos en formato de columnas: unique_id, ds y y.

data = pd.read_csv("ipc_honduras.csv",  parse_dates=['Date']) 
data.tail()
Date Valor
371 2022-12-01 9.80
372 2023-01-01 8.93
373 2023-02-01 9.80
374 2023-03-01 9.05
375 2023-04-01 7.44 
# Exploremos la serie graficamente
sns.lineplot(data = data, x = "Date", y = "Valor", label = "Inflación",
             color = "lime")
plt.xlabel("Fecha")
plt.ylabel("% Inflación")
plt.title("Variación Interanual Honduras 1992-2023")
plt.show()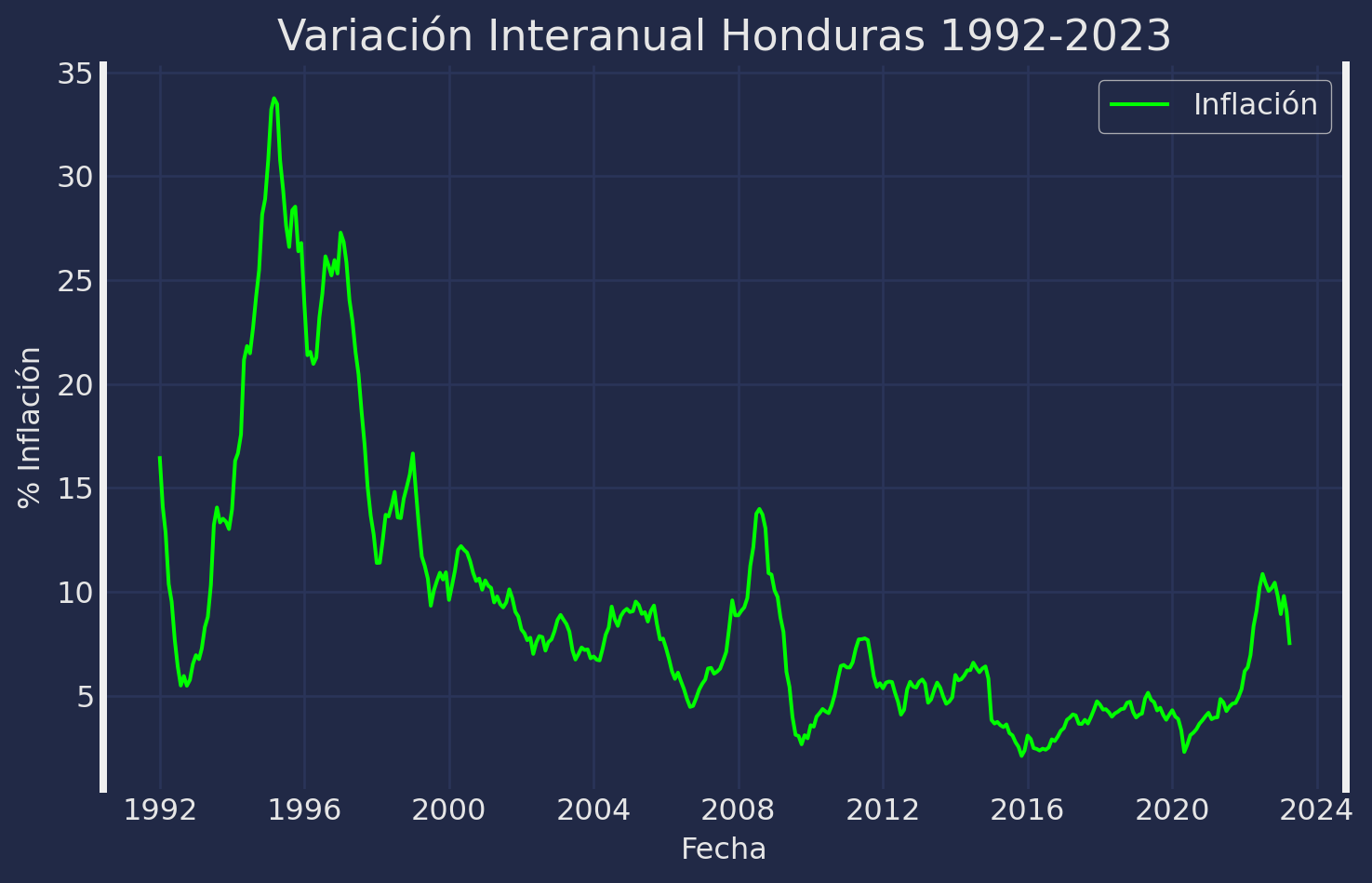

Transformando los datos al formato MLForecast

datos = data.copy()
datos = data[["Date", "Valor"]]
print(datos.shape)

datos["unique_id"] = "1"
datos.columns = ["ds", "y", "unique_id"]
datos.head()
(376, 2)
ds y unique_id
0 1992-01-01 16.53 1
1 1992-02-01 14.09 1
2 1992-03-01 12.83 1
3 1992-04-01 10.37 1
4 1992-05-01 9.52 1

Creando el Modelo

models = [
    #lgb.LGBMRegressor(),
    xgb.XGBRegressor(),
    #RandomForestRegressor(random_state=0)
]

modelo = MLForecast(
    models = models, 
    freq = "MS",
    lags = [1,12],
    lag_transforms = {
        1: [expanding_mean],
        12:[(rolling_mean,5)]},
    differences=[12],
    date_features = ["month", "year"]
    )
    
modelo.fit(datos, id_col = "unique_id", time_col = "ds", target_col = "y")
MLForecast(models=[XGBRegressor], freq=<MonthBegin>, lag_features=['lag1', 'lag12', 'expanding_mean_lag1', 'rolling_mean_lag12_window_size5'], date_features=['month', 'year'], num_threads=1)

Estamos listos para poder realizar las predicciones, en este caso, vamos a pronosticar 8 pasos adelante, es decir, 8 fechas a futuro comenzando a partir del 2023-05-01 a 2023-12-01

preds = modelo.predict(8)
preds
unique_id ds XGBRegressor
0 1 2023-05-01 6.524219
1 1 2023-06-01 5.673842
2 1 2023-07-01 5.086069
3 1 2023-08-01 4.643029
4 1 2023-09-01 4.179777
5 1 2023-10-01 4.326499
6 1 2023-11-01 4.554456
7 1 2023-12-01 4.326124

Veamos visualmente nuestros pronósticos

pd.concat([datos, preds]).set_index("ds").plot(figsize = (9,6));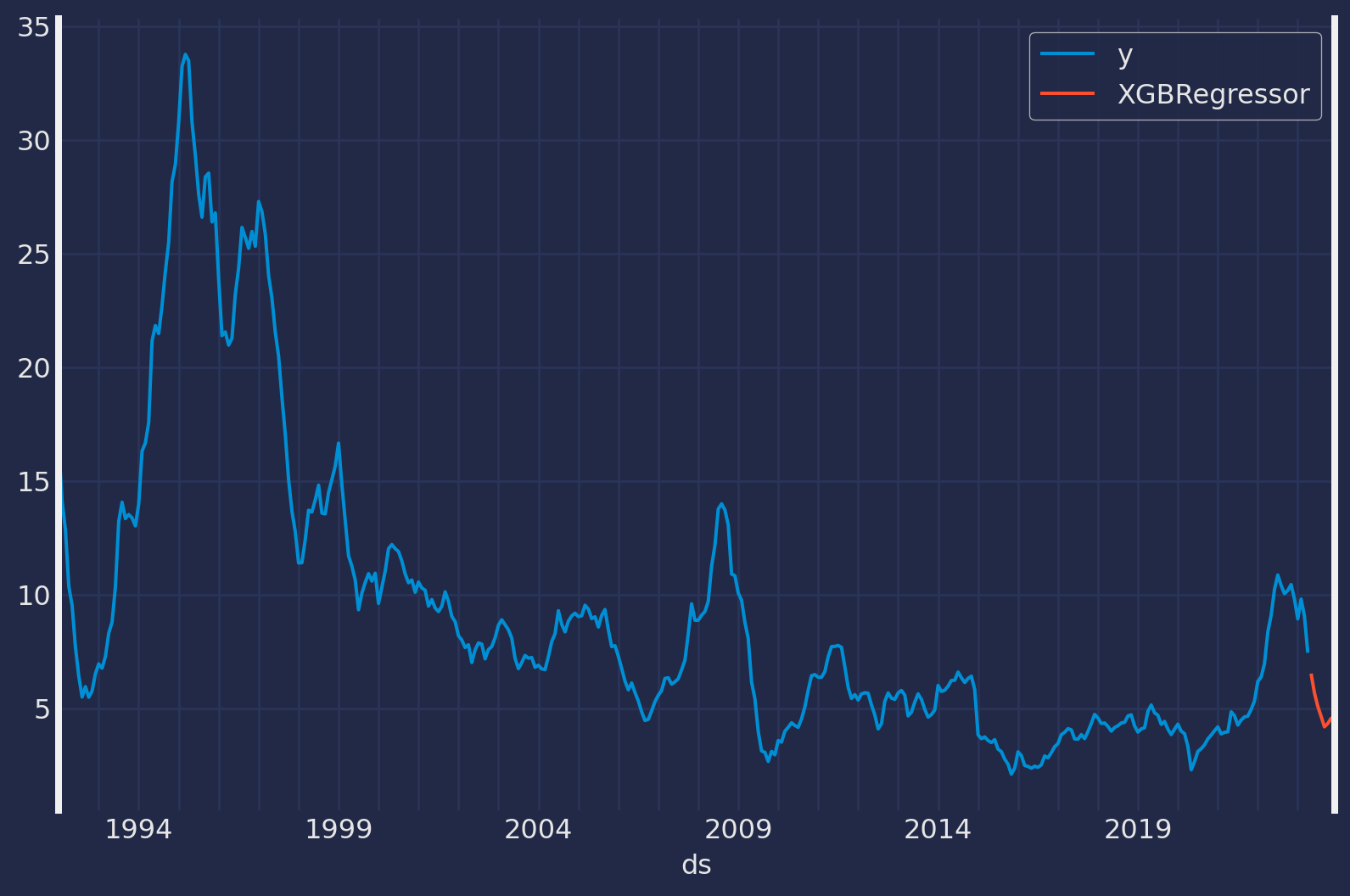

Predicción de Intervalos

Con MLForecast, puede generar intervalos de predicción. Para configurar la predicción, debe pasar una instancia de la clase PredictionIntervals a la clase prediction_interval el cual es un argumento del método .fit.

La clase toma tres parámetros: n_windows, h y method.

  • n_windows representa el número de ventanas de validación cruzada utilizadas para calibrar los intervalos.

  • h es el horizonte de pronóstico

  • method puede ser conformal_distribution o conformal_error

Tenga en cuenta que se deben utilizar mínimo 2 ventanas de validación cruzada.

from mlforecast.utils import PredictionIntervals
modelo.fit(
    datos, 
    prediction_intervals=PredictionIntervals(n_windows=9, h=8)
);

Después de eso, solo tiene que incluir los niveles de confianza deseados en el predict u sando el argumento level. Los levels deben estar entre 0 y 100.

predictions_w_intervals = modelo.predict(8, level=[95]) 
predictions_w_intervals.head()
unique_id ds XGBRegressor XGBRegressor-lo-95 XGBRegressor-hi-95
0 1 2023-05-01 6.524219 5.193575 7.854862
1 1 2023-06-01 5.673842 4.591230 6.756455
2 1 2023-07-01 5.086069 3.446764 6.725373
3 1 2023-08-01 4.643029 1.342779 7.943279
4 1 2023-09-01 4.179777 -0.042535 8.402088 
predictions_w_intervals.set_index("ds").plot(figsize = (8,6));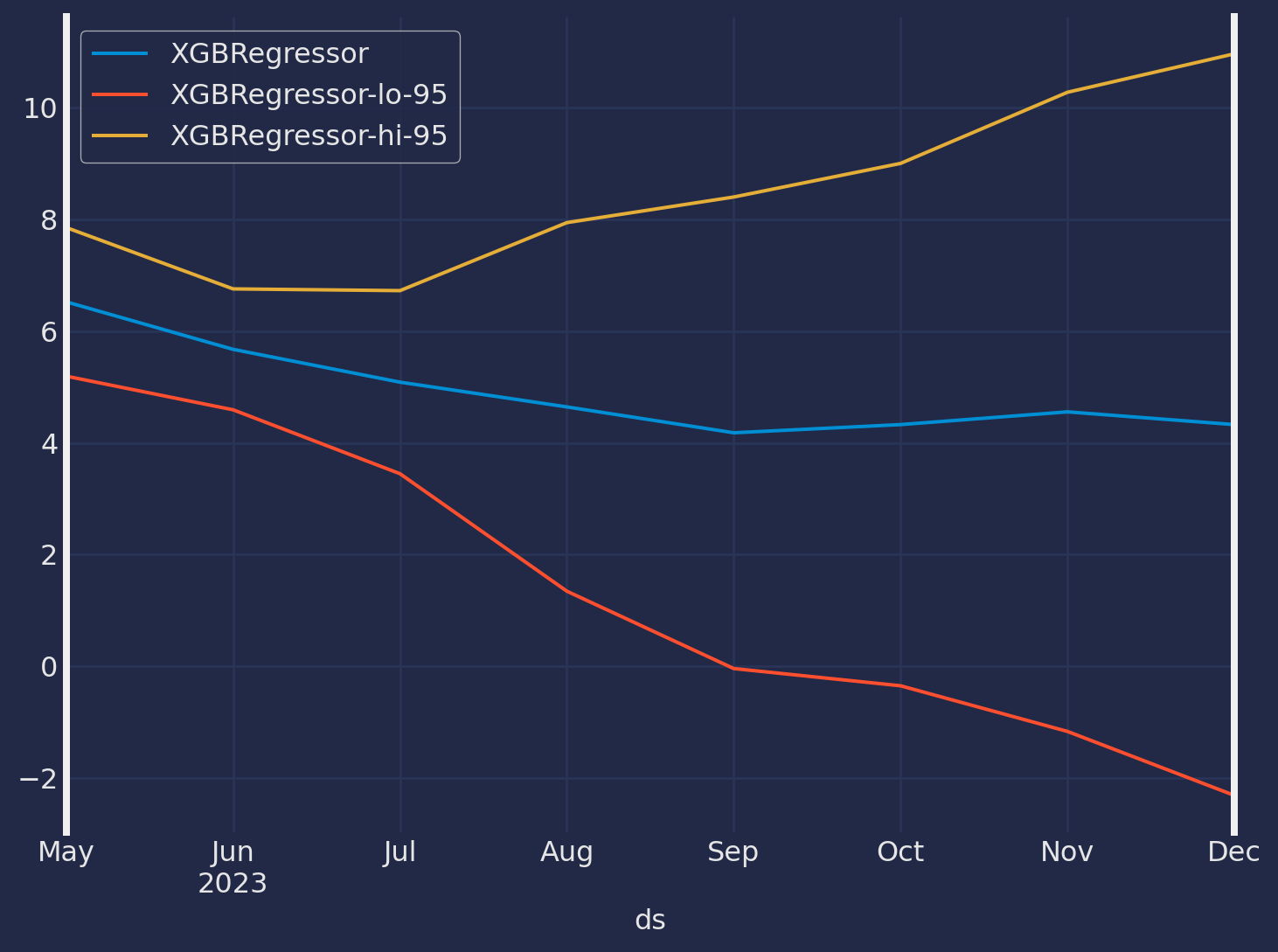

Note que las bandas de confianza para los primeros tres meses de pronóstico no son tan anchas, sin embargo, a medida que vemos mas lejos la incertidumbre se hace aún mayor, eso es lo que podemos apreciar con las bandas de confianza.

Referencias

Rob J.Hyndman y George Athanasopoulos (2018). “Principios y Prácticas de pronósticos, validación cruzada de series de tiempo”

https://nixtla.github.io/mlforecast/forecast.html